Topological Sorting

Problem Statement:
        Implement Topological Sorting, for the given Directed Acyclic Graph (DAG)

Fig: Directed Acyclic Graph(DAG)

Solution :

Note: Graph should be Directed Acyclic Graph (DAG)

Full Source Code : Link

What is Topological ordering or topological sort ?

Topological Sorting aka Toposort or Topological Ordering of a directed graph is a linear ordering of its vertices .i.e. all the directed edges of the graph should go forward in the ordering.

You can consider an example of Semester courses where you have a lot a courses to study but there are few per-requisite course required before you attempt for advanced ones.

A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG).

The topological sort of the given above graph would produce the given below figure in which all the edges go forward.

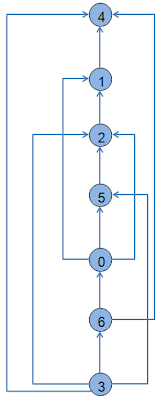Fig: DAG , in which all edges go forward

  ///======== TOPOLOGICAL SORT ========/////////
 // to keep track of ordering
 private int currentLabel;
 int[] sortedArray;
 public void topologicalSort()
 {

  currentLabel=vistedStatusList.size()-1;
  sortedArray=new int[numVertices];

  Set<Map.Entry<Integer, Boolean>> set=vistedStatusList.entrySet();
  Iterator<Map.Entry<Integer, Boolean>> iterator=set.iterator();
  while(iterator.hasNext())
  {
   Map.Entry<Integer,Boolean> node= iterator.next();
   int key=node.getKey();
   boolean isVisited=vistedStatusList.get(key);
   if(!isVisited)
    topologicalSortUtil(key); // Call DFS for a given node , if unvisited
  }

  // printing the topological sorted array
  for(int i=0;i<sortedArray.length;i++)
  {
   if(sortedArray[i]!=0)
    System.out.print(sortedArray[i]+"\t");
  }
 }


 /**
  * Procedure Similar to DFS, unwinds when deepest node is encountered
  * @param vertex
  */
 public void topologicalSortUtil(int vertex)
 {
  vistedStatusList.put(vertex,true);
  List<Integer> list=adjList.get(vertex);

  if(list!=null)
  {
   int size= list.size();
   for(int i=0;i <size; ++i)
   {
    int adjNode=list.get(i);
    boolean isVisited=vistedStatusList.get(adjNode);
    if(!isVisited)
    {
     //System.out.println(adjNode + "\t");
     topologicalSortUtil(adjNode);
    }
   } 
  }
  /* for loop will end when the sink vertex is reached , that sink vertex is plucked and put in the array as per the currentLabel, 
   * which corresponds to its position in topological sort */
  sortedArray[currentLabel]=vertex;
  currentLabel--;
 }
  

Time Complexity : O(m+n)
where m: number of edges
           n: number of vertices

Please post comments and suggestions.

Happy Coding !! :)