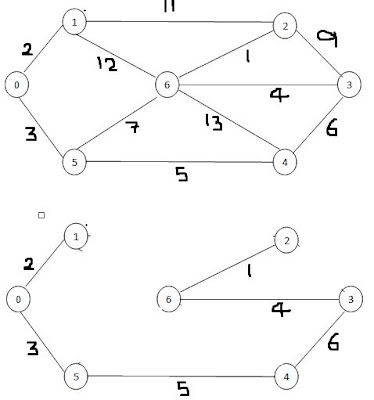
Problem Statement : Given below is a Graph of which calculate MST using Kruskal's MST
Solution:
The MST calculated from the first figure is shown in the second figure.
Kruskal's Algorithm:
In this algorithm all the edges are sorted in cost order firstly , then the minimum of the given set of edges is picked such that cycles are not formed , until minimum spanning tree is complete. Union Find data structure is used to determine if a cycle is formed when an edge is picked.
Union Find data structure introduces two operations
1. Union(int vertex1 , int vertex2) : This operation merges the two clusters headed by vertex1 and vertex2.
2. Find(int vertex) : This operation returns the parent/leader of the cluster in which the given vertex lies.
File Name: Graph.java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 | import java.util.ArrayList; import java.util.Collections; import java.util.List; /** * Kruskal's Edge definition * @author Prateek * */ class Edge implements Comparable<Edge>{ int src; int dest; int weight; public Edge(int src,int dest,int weight) { this.src=src; this.dest=dest; this.weight=weight; } @Override public String toString() { return "Edge: "+src+ " - " + dest + " | " +" Weight: "+ weight; } @Override public int compareTo(Edge another) { return this.weight - another.weight; } } /** * Kruskal's MST graph * @author Prateek * */ public class Graph { private int mNumVertices; // Number of vertices in the graph private int mNumEdges; // Number of edges in the graph // Input Edge List private List<Edge> mEdgeList; // Processed Edge List of Kruskal Algo private List<Edge> mResultantEdgeList; public Graph(int numVertices,int numEdges) { this.mNumVertices=numVertices; this.mNumEdges=numEdges; this.mEdgeList=new ArrayList<Edge>(numEdges); this.mResultantEdgeList=new ArrayList<Edge>(mNumVertices-1); } /** * Kruskal's Subroutine to find MST */ private void KruskalMST() { // sort the edge list Collections.sort(mEdgeList); UnionFind uf=new UnionFind(mNumVertices); // Iterating over the sorted input edgeList for(int i=0;i<mNumVertices;i++) { Edge edge=mEdgeList.get(i); int v1 = uf.Find(edge.src); //parent vertex for source int v2 = uf.Find(edge.dest); //parent vertex for destinition // if parents do not match, consider edge list for MST and , union the two vertex if(v1!=v2) { mResultantEdgeList.add(edge); uf.Union(v1, v2); } } // print the final MST printKruskalEdges(); } /** * Printing the Kruskal MST edges */ private void printKruskalEdges() { for(Edge edge:mResultantEdgeList) { System.out.println(edge); } } public static void main(String[] args) { Graph graph=new Graph(7, 11); graph.helper(); } public void helper() { mEdgeList.add(new Edge(0, 1, 2)); mEdgeList.add(new Edge(0, 5, 3)); mEdgeList.add(new Edge(1, 2, 11)); mEdgeList.add(new Edge(1, 6, 12)); mEdgeList.add(new Edge(2, 6, 1)); mEdgeList.add(new Edge(2, 3, 9)); mEdgeList.add(new Edge(3, 6, 4)); mEdgeList.add(new Edge(3, 4, 6)); mEdgeList.add(new Edge(4, 6, 13)); mEdgeList.add(new Edge(4, 5, 5)); mEdgeList.add(new Edge(5, 6, 7)); KruskalMST(); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 | /** * Union-Find DS node * @author Prateek * */ class UFNode { int parent; // parent of Vertex at i in the nodeHolder int rank; // Number of object present in the tree/ Cluster UFNode(int parent, int rank) { this.parent = parent; this.rank = rank; } } /** * Union-Find Data structure * @author Prateek * */ public class UnionFind { // Node Holder haveing UFNode private UFNode[] nodeHolder; // number of node private int count; public UnionFind(int size) { if (size < 0) throw new IllegalArgumentException(); count = size; nodeHolder = new UFNode[size]; for (int i = 0; i < size; i++) { nodeHolder[i] = new UFNode(i, 1); // default values, node points to // itself and rank is 1 } } /** * Finds the parent of a given vertex, using recursion * * @param vertex * @return */ public int Find(int vertex) { if (vertex < 0 || vertex >= nodeHolder.length) throw new IndexOutOfBoundsException(); if (nodeHolder[vertex].parent != vertex) nodeHolder[vertex].parent = Find(nodeHolder[vertex].parent); return nodeHolder[vertex].parent; } public int getCount() { return count; } /** * @param v1 * : vertex 1 of some cluster * @param v2 * : vertex 2 of some cluster * @return true if both vertex have same parent */ public boolean isConnected(int v1, int v2) { return Find(v1) == Find(v2); } /** * unions two cluster of two vertices * @param v1 * @param v2 */ public void Union(int v1, int v2) { int i = Find(v1); int j = Find(v2); if (i == j) return; if (nodeHolder[i].rank < nodeHolder[j].rank) { nodeHolder[i].parent = j; nodeHolder[j].rank = nodeHolder[j].rank + nodeHolder[i].rank; } else { nodeHolder[j].parent = i; nodeHolder[i].rank = nodeHolder[i].rank + nodeHolder[j].rank; } count--; } } |
No comments:
Post a Comment